TopoJSON est un format cartographique astucieux. Très compact, il passe plus facilement sur le web. Topologique, il décrit les relations de voisinage entre territoires et facilite toutes sortes de traitements : reprojections, agrégations géométriques, lissages, généralisations, anamorphoses…
TopoJSON constitue une ré-implémentation moderne, optimisée pour le web, d’une vieille idée, celle de la représentation topologique en cartographie. Bien que posé en 2012 (Mike Bostock/D3), TopoJSON est encore peu employé à sa juste valeur. Cet article détaille ses avantages et aborde comment le générer et l’utiliser.
Voici tout d’abord les idées-clés à retenir, elles seront traduites en programmes plus concrets (R, Javascript) dans de futurs articles.
Compacité
Jusqu’à trois fois plus léger que d’autres formats textes, il permet de valoriser en ligne, dans un navigateur, des fonds de carte plus volumineux. Par exemple le maillage des communes de France, dont le volume compressé peut être réduit à moins de 3 Mo.
| GeoJSON | TopoJSON | GeoJSON compressé | TopoJSON compressé |
|---|---|---|---|
| 24 | 9 | 7 | 2,5 |
Intégrité topologique
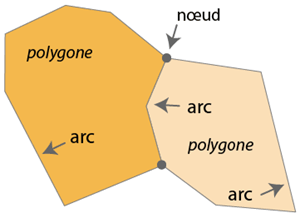 Posons tout d’abord quelques définitions de topologie : dans un maillage polygonal, un nœud est un point de rencontre entre 3 segments ou plus, un arc une portion de tracé entre deux nœuds. Un polygone peut se décomposer en arcs. Dans la figure ci-contre, chacun des deux polygones se réduit à deux arcs.
Posons tout d’abord quelques définitions de topologie : dans un maillage polygonal, un nœud est un point de rencontre entre 3 segments ou plus, un arc une portion de tracé entre deux nœuds. Un polygone peut se décomposer en arcs. Dans la figure ci-contre, chacun des deux polygones se réduit à deux arcs.
2 territoires sont voisins (ou contigus ou limitrophes) quand ils partagent une même frontière (ou un même arc), ce qui est caractéristique d’un maillage dont tous les éléments s’emboîtent parfaitement.
Adjacences, inclusions, typologie de formes, bordures…
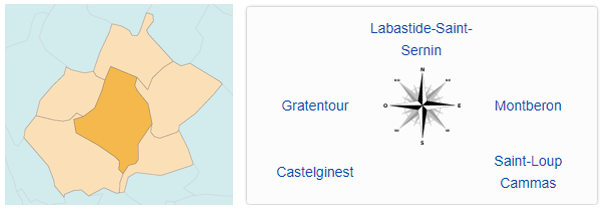
Le format topologique permet d’établir facilement la liste des territoires limitrophes d’une entité. Il est pratique de trier cette liste par azimuth croissant, comme le fait Wikipedia de façon purement topologique, sans indiquer de façon précise les distances ou les angles.
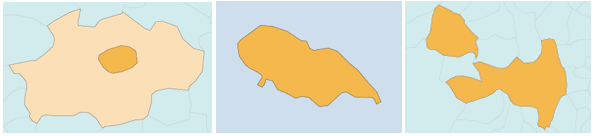
La topologie s’intéresse aux relations d’adjacence et d’inclusion, et aussi aux formes. Elle distingue par exemple les entités trouées, ou à l’inverse enclavées, ou isolées comme peut l’être une île, ou en plusieurs parties. Avec le format topologique, il est facile d’identifier toutes les communes possédant chacune de ces particularités.
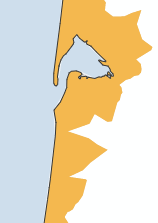 Envie de lister toutes les communes littorales et/ou frontalières ? C’est aussi possible par l’entremise d’un raisonnement purement topologique, où l’on s’attache à distinguer la notion de « bord » de la notion de « ligne de démarcation » entre territoires. Si dans une commune on détecte un arc qui n’est pas partagé avec une autre commune, c’est qu’on a affaire à une commune « en bordure », dont certaines limites sont aux marges du maillage.
Envie de lister toutes les communes littorales et/ou frontalières ? C’est aussi possible par l’entremise d’un raisonnement purement topologique, où l’on s’attache à distinguer la notion de « bord » de la notion de « ligne de démarcation » entre territoires. Si dans une commune on détecte un arc qui n’est pas partagé avec une autre commune, c’est qu’on a affaire à une commune « en bordure », dont certaines limites sont aux marges du maillage.
Il est en revanche plus difficile de distinguer une commune littorale d’une commune frontalière, d’autant que ces deux concepts ne sont pas exclusifs. Hendaye est littorale, mais a aussi une frontière avec l’Espagne.
Généralisation/simplification
Simplifier le contour d’un territoire, c’est assez facile en retirant du tracé un point de temps en temps. Le défi consiste à maintenir ce-faisant la cohérence du découpage, ce que peu de logiciels cartographiques savent réaliser, faute de maîtriser la décomposition topologique. En simplifiant chaque arc plutôt que chaque périmètre indépendamment des autres, la topologie est préservée.
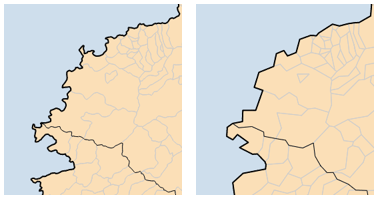
Anamorphose
Cette transformation déforme le contour des territoires en simulant l’application d’un champ de forces sur chacun des points des tracés. Ce champ résulte de la distribution d’une valeur statistique. Celle-ci, généralement non uniforme, va donc agir de façon différenciée dans l’espace. Ce calcul est souvent lourd et convoque plusieurs itérations. Le format topologique permet de l’accélérer, et par conséquent d’appliquer l’anamorphose à des fonds de carte plus volumineux.
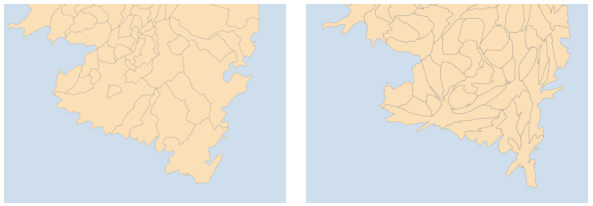
Reprojection
Projeter, ou changer de système de coordonnées, peut s’appliquer indépendamment à chaque territoire sans que l’adjacence ne soit altérée, puisque le nombre de points de chaque tracé reste le même. Deux points qui coïncidaient avant transformation mathématique coïncideront après. Comme pour l’anamorphose, il s’agit avec le format topologique de gagner en rapidité (pratiquement d’un facteur deux).
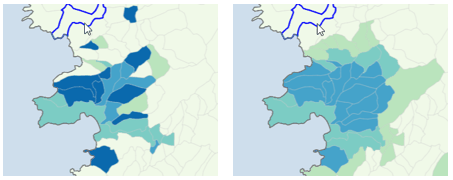
Recherches rapides dans un voisinage, lissages
L’accès rapide aux voisins facilite l’identification du territoire survolé par la souris. L’algorithme peut commencer par une identification imprécise, et conduire un test plus décisif (pointInPolygon) sur le champ réduit des territoires « voisins » de cette localisation. C’est ainsi que l’on peut garantir par exemple une bonne fluidité de l’affichage correct de l’infobulle, même quand le pointeur de la souris se déplace rapidement.
Une autre application de l’accès au voisinage consiste à associer un disque spatial mobile au calcul d’un indicateur (typiquement un taux), étendant à deux dimensions le principe du lissage par moyenne mobile habituellement appliqué à une série temporelle. Pour bien faire, on identifiera par couronnes successives les territoires dont le chef-lieu est dans un rayon donné, en appliquant une pondération inverse à la distance.
Regroupements par dissolution des frontières intérieures
Les polygones étant décomposés en arcs, leur fusion géométrique devient triviale. Elle élimine les frontières intérieures en ne gardant que les frontières extérieures. Comment distinguer les deux types de frontières ? Une frontière intérieure est utilisée deux fois dans le dessin (par deux territoires limitrophes), alors qu’une frontière extérieure n’est parcourue qu’une fois.
Esthétique du rendu cartographique
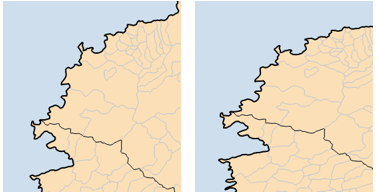
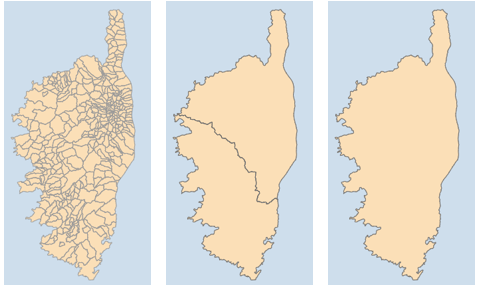
L’analyse topologique ne sert pas qu’à accélérer les traitements mathématiques ou les dessins, elle les rend aussi plus esthétiques ! Considérons une couche des contours départementaux, que l’on voudrait exposer de façon claire. Si on la construit à partir de polygones départementaux, les limites entre deux départements sont dessinées deux fois, et elles vont ainsi paraitre plus épaisses ou foncées, comme si le stylo parcourait deux fois le même tracé (image de gauche).
En revanche, si cette couche est décomposée topologiquement en arcs élémentaires, ceux-ci vont produire un tracé homogène, qu’il s’agisse de limites entre départements ou de bordures littorales, sans aucune redondance de segments. Mieux encore : la décomposition topologique distingue les arcs intérieurs des arcs de bordure, ce qui permet de les dessiner différemment, par exemple (image de droite) avec un contour plus foncé pour le tracé extérieur.
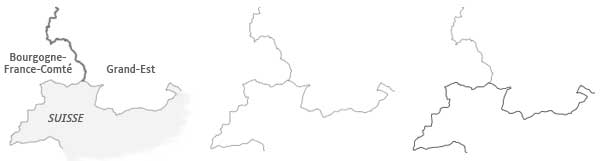
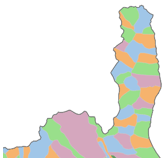 Une autre exploitation des relations de voisinage consiste à colorier un maillage en faisant en sorte que deux territoires adjacents n’aient jamais la même couleur. C’est une façon élégante de présenter un zonage, sans y rapporter de donnée statistique particulière. Un théorème édicte que 4 couleurs seulement sont nécessaires pour paver tout l’ensemble. Les algorithmes les plus rapides mobilisent en pratique jusqu’à 6 couleurs, ce qui reste très raisonnable.
Une autre exploitation des relations de voisinage consiste à colorier un maillage en faisant en sorte que deux territoires adjacents n’aient jamais la même couleur. C’est une façon élégante de présenter un zonage, sans y rapporter de donnée statistique particulière. Un théorème édicte que 4 couleurs seulement sont nécessaires pour paver tout l’ensemble. Les algorithmes les plus rapides mobilisent en pratique jusqu’à 6 couleurs, ce qui reste très raisonnable.
Structure du format de description topologique
avec TopoJSON
TopoJSON est un format texte avec lequel je peux décrire entièrement un fond de carte, par exemple un maillage communal. Mais à la différence du standard GeoJSON, il va distinguer :
- une information purement géométrique : elle est déclinée par arc, c’est-à-dire que pour chaque arc un vecteur exprime la suite des points (coordonnées x/y) de son tracé. Le fond de carte de la France et ses 35 000 communes peut ainsi se décomposer en 104 000 arcs ;
- une information purement topologique : on s’intéresse cette-fois-ci aux polygones, définis chacun comme une suite d’arcs. Un polygone est décrit par un vecteur de petits numéros (les indices d’arcs), certains pouvant être négatifs, on va voir tout de suite pourquoi.
Prenons un exemple très simple avec les deux départements de Corse, qui peuvent être décrits par 3 arcs numérotés de 0 à 2, dont le premier est la frontière entre 2A et 2B. La Corse-du-Sud (2A) réunit les arcs 0 et1, tandis que la Haute-Corse (2B) mobilise les arcs 0 et 2.
Mais un programme de dessin a besoin d’une information supplémentaire : le sens de parcours, typiquement celui des aiguilles d’une montre. Chaque arc est par nature orienté : en tant que suite de points, il a un début et une fin. On voit que pour 2A, les 2 arcs 0 et 1 s’enchainent naturellement. Mais pas pour 2B : il faudrait par exemple commencer avec l’arc 2 et remonter l’arc 0 dans l’autre sens.
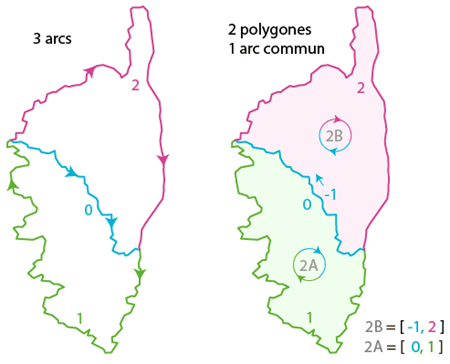
l'arc frontière (en bleu) est parcouru dans un sens, puis dans un autre
Pour traduire cette idée d’un arc à parcourir dans le sens inverse, on utilise une valeur négative d’indice d’arc. La petite délicatesse est que comme les indices positifs commencent à 0 : 0, 1, 2… les indices négatifs vont eux commencer à -1 : -1, -2, -3. Ainsi le « négatif » de 0 est -1, celui de 1 est -2, etc. Il y a un décalage de 1 à prendre en compte quand on référence un arc à parcourir en sens inverse.
Une fois ceci compris, on peut décrire chaque polygone avec ces indices d’arc, en ayant en tête que 0 et -1 désignent le même arc, tout comme 2 et -3.
Si maintenant, considérant un arc donné, d’indice absolu n, je veux identifier les polygones qui l’utilisent, il me suffit de partir à la recherche des indices n ou -n-1. C’est ainsi que, de fil en aiguille, considérant par exemple une commune et les indices absolus d’arc qui la définissent, je vais identifier les polygones qui ont avec elle un arc en commun, et qui sont donc ses voisins.
Quelques pistes algorithmiques
J’exposerai plus en détail comment procéder dans de prochains articles. Voici en guise d’apéritif quelques idées à traduire en code.
Entités à trous
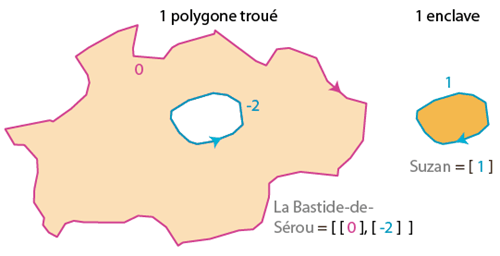
La Bastide-de-Sérou (09) encercle une autre commune, celle de Suzan. Ces deux communes ont un arc en commun (d’indice 1 ou -2). La Bastide a deux arcs, qui sont aussi deux « rings » fermés. La convention pour qu’un trou apparaisse dans un tel multi-polygone est que le sens de ces anneaux diffère (typiquement clockwise pour le ring principal, anti-clockwise pour le trou). Ce trou correspond à la commune de Suzan, décrite par un indice d’arc opposé. Rappel : -2 et 1 désignent le même arc, mais de façon inversée.
Un multi-polygone se reconnait à ce que son vecteur d’arcs est un vecteur de vecteurs (voir les crochets emboîtés). La définition de Suzan se retrouve dans la définition de La Bastide-de-Sérou, à cela on identifie la paire que forment une commune trouée et une autre enclavée.
Pour rendre la comparaison plus évidente, il est utile de passer les indices d’arc en « valeur absolue » (au décalage de 1 près lors du changement de signe). Ainsi la définition simplifiée de La Bastide-de-Sérou devient : [ [ 0 ], [ 1 ] ] à comparer avec [ 1 ] pour Suzan. On voit bien que la première englobe la seconde.
Entités isolées
Très simple ici, il s’agit d’une entité sans voisins identifiés. On retrouve là essentiellement des îles.
Entités en plusieurs parties distinctes
On peut l’approcher comme une entité multi-polygonale qui ne serait pas trouée…
Comment utiliser TopoJSON
J’exposerai plus en détail comment procéder dans de prochains articles. Mais pour commencer à jouer avec TopoJSON, il faut d’abord être en mesure de générer ce format, ou d’accéder à des fichiers déjà constitués. Mapshaper exporte très rapidement vers TopoJSON un fichier de format d’origine shapefile ou GeoJSON. Il est aussi en mesure de lire tout fichier TopoJSON, de le visualiser et de procéder à quelques traitements topologiques : généralisations, fusions géométriques.
La librairie D3 offre de très utiles fonctions en complément, dont un calcul de la liste des voisins de chaque entité d’une couche (cf. topojson.neighbors()). Elle sait dessiner une carte en Javascript, et donc dans un navigateur, à partir d’un fichier TopoJSON.
Outre mapshaper et D3, de nombreuses technologies peuvent exploiter TopoJSON en mode web ou bureautique : D3/Observable, Magrit, Khartis, Datawrapper, PowerBI… Géoclip valorise également un format topologique en reprenant les principes du TopoJSON dans un format binaire encore plus compact.
Voici pour les curieux d’une implémentation concrète un premier aperçu, sous forme de jeu topologique, mais grandeur réelle.
Ce fichier CSV présente une série d’informations topologiques pour chaque commune de France, en 2020 : liste des voisins triée par azimuth, territoires enclavés, troués, en bordure… Nous verrons ultérieurement comment il a été élaboré à partir du fichier TopoJSON.
Récapitulatif
TopoJSON est un format de description de couches cartographiques, typiquement des maillages administratifs. Facile à générer et à lire, puisque textuel, Il est optimisé pour une exploitation en ligne, dans un navigateur.
Décomposant les formes en arcs élémentaires, il accélère les traitements géométriques par des boucles plus courtes, tout en maintenant la contiguïté initiale des entités. Il facilite également généralisations et regroupements géométriques.
Informant sur la topologie, c’est-à-dire les relations d’adjacence entre territoires, il permet enfin des analyses spatiales originales.
Pour en savoir plus sur le format topologique
et TopoJSON
Le concept de topologie dans les systèmes d’information géographique n’est pas neuf. Il est même, paradoxalement, fondateur de la discipline.
ARC/INFO, le premier logiciel SIG moderne, valorisait dès les années 1980 un format de « couvertures » décrivant et garantissant l’intégrité topologique, érigée à l’époque comme valeur cardinale.
Ces principes ont quelque peu perdu de leur vigueur avec la naissance du format Shapefile, à l’occasion de la sortie d’ArcView 2 (Esri) au début des années 1990. Shapefile n’est pas topologique, Esri l’a conçu comme une alternative plus démocratique. Il offrait à l’époque bien plus de souplesse que le format topologique d’ARC/INFO : pour digitaliser en masse et afficher rapidement les cartes sur les ordinateurs de l’époque.
Car l’intégrité topologique amène beaucoup de contraintes de saisie et impose un peu de calcul pour reconstituer des polygones et les dessiner à l’écran.
Avec le web et la montée en puissance de la cartographie statistique, la topologie, sa compacité, sa flexibilité reprennent des couleurs, d’autant que les fonds de carte administratifs supports de datavisualisations sont généralement produits par des organismes soucieux de qualité …topologique.
TopoJSON a été formalisé, pour des besoins concrets de publication web, par Mike Bostock, à l’époque data-journaliste au New-York-Times, par ailleurs chercheur en datavisualisation, concepteur et programmeur de génie. Outre la description topologique, il incorpore des astuces complémentaires pour réduire encore la taille des fichiers (quantization, delta-encoding). Bostock s’est aussi inspiré des travaux antérieurs de Mark Harrower et Matthew Bloch, créateurs du toujours fringant mapshaper, construit lui-aussi autour d’un mécanisme de décomposition topologique.
Merci pour cet article clair et très éclairant ! J’y ai trouvé, à la deuxième lecture, la clé d’une incompréhension qui m’empêchait d’avancer : la différence d’indexation entre le sens positif dans lequel les arcs commencent au numéro 0 et le sens négatifs, dans lequel les indices commencent à -1 !
Merci pour cette précision de commentaire, je me suis moi même longtemps emmêlé les pinceaux su ce sujet !