Deux exigences opposées tiraillent le cartographe : schématiser pour mieux imprimer les messages essentiels, ou délivrer le maximum de détails, tant que l’image le permet. Ces exigences ne sont pas forcément contradictoires.
En cartographie thématique, l’art de la coloration repose d’abord sur le découpage en classes, ce que l’on appelle discrétiser. Les bons logiciels proposent plusieurs méthodes automatiques : quantiles, intervalles égaux et Jenks (ou seuils naturels) sont les plus fréquentes.
La discrétisation Head/tail, proposée en 2013 par le géographe Bin Jiang, et récemment mise en lumière en France par Thomas Ansart dessine fort bien les données hiérarchisées, dont la distribution dissymétrique comprend typiquement beaucoup de petites valeurs et quelques valeurs élevées. C’est le cas par exemple de la population des communes, des revenus moyens, ou des loyers.
Voici une première illustration, avec le coût par m² du loyer mensuel des appartements par commune et arrondissement en France, en 2023.
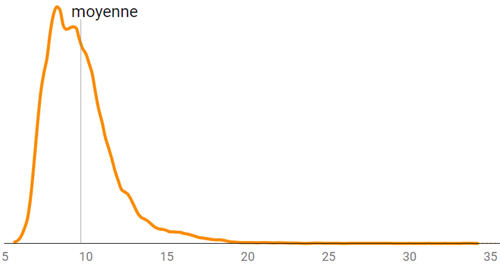
Head/tail à gauche prend la moyenne comme premier seuil, considère les données supérieures (head), puis calcule de façon itérative des moyennes emboitées.
La méthode de Jenks est également itérative. Elle délimite x groupes les plus homogènes possibles, et en même temps les plus distincts les uns des autres. Elle est proche dans l’esprit de la méthode des K-moyennes.
Ces différentes méthodes aspirent à déterminer des « seuils naturels », des ruptures inhérentes aux données plutôt qu’imposées de l’extérieur par des intervalles égaux ou des effectifs égaux (quantiles). Elles sont puissantes et complémentaires.
Head/tail assume de simplifier drastiquement la représentation en neutralisant la première partie de la distribution, celle sous la moyenne (le tail). Ce qui permet de mieux dégager la hiérarchie des valeurs supérieures à la moyenne (head).
J’aime beaucoup ce rendu plus doux, moins agressif, tout en nuances, en particulier pour les loyers dans le bassin parisien. La structure hiérarchique que cette carte dessine, avec une belle séparation de l’avant-plan et de l’arrière-plan, s’imprimera plus durablement dans mon esprit.
Comparons aussi avec cette version (je suppose par quantile), palette divergente, de Boris Mericskay, avec des données de même origine. L’opposition vert/violet a le mérite de simplifier fortement l’information, divisant la France en deux ou trois, autour d’une classe centrale, d’une moyenne supposée faire sens.

Mais quand la distribution est déséquilibrée comme celle des loyers, une représentation symétrique est moins pertinente. Par exemple, une très faible variation du 1er seuil, intervenant dans la pente abrupte du début de la distribution, fera basculer beaucoup de communes d’une classe verte à l’autre, avec un effet violent sur la répartition colorée des deux premières classes. Et le vert foncé n’est pas le symétrique du violet foncé, il ne traduit pas le même écart à la moyenne.
Voici 3 autres illustrations statistiques et cartographiques de l’intérêt de la méthode Head/tail, appliquée toujours à des distributions dissymétriques, avec beaucoup de petites valeurs et peu de grandes valeurs.
1 – La densité de population (2021) – source Insee
Avec Head/tail, Paris, puis Lyon, sont distinguées du groupe des autres villes moyennes (Toulouse, Bordeaux, Nantes, Nice, etc.).
2 – La médiane du niveau de vie (2021) – source Insee
La frontière suisse, une partie de la frontière luxembourgeoise, l’ouest de l’Île-de-France et le sud de l’Oise sautent davantage aux yeux, du fait d’un meilleur contraste.
3 – La part des diplômés d’un BAC+5 ou plus dans la pop. non scolarisée de 15 ans ou plus (2021)
– source Insee
Pour un plus large usage de Head/tail
Bin Jiang rappelle que dans la nature, le monde du vivant, les organisations humaines, les phénomènes observés se présentent rarement sous forme d’une distribution symétrique autour d’une « moyenne ». Il y a en général plus de petites valeurs que de grandes.
Mais la hiérarchie déroulée à partir des grandes valeurs est ce qui frappe tout d’abord l’esprit, ce qui donne une première idée d’une structure d’ensemble : hiérarchie des villes, des longueurs de rues dans une ville, des entreprises dans un secteur donné, des intensités de tremblements de terre, de répartition des richesses, de popularité des sites web, de fréquence des mots dans un texte, etc.
Ou les niveaux successifs d’organisation d’une feuille, de ses nervures :
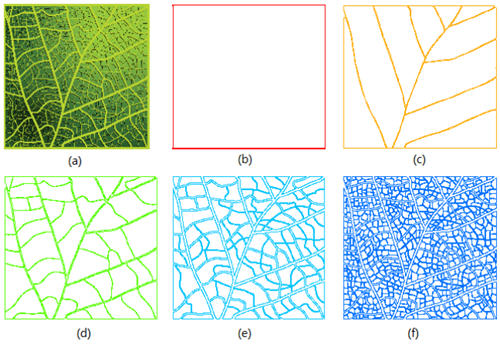
Pour employer un langage plus technique, les phénomènes naturels ou géographiques sont peu souvent gaussiens (symétriques), plus souvent « paretiens » (de Pareto et sa fameuse loi des 80/20 – 20 % des causes expliquent 80 % des effets), ou « log-normaux » (leur logarithme est gaussien).
Pour Jiang, le nombre de seuils calculés par la méthode Head/tail (dénommé ht index) est un indicateur de la profondeur organisationnelle du phénomène étudié (il le rapproche même du concept de dimension fractale, posé par Benoît Mandelbrot).
Pour une distribution symétrique, idéale, quasi-gaussienne, le ht index sera souvent faible, 2 par exemple. À l’inverse, un ht-index > 5 caractérisera un phénomène étagé, où parfois même, d’un niveau à l’autre, l’on retrouve les mêmes rapports d’échelle.
Description de l'algorithme Head/Tail
Pour découvrir l’algorithme en action (JavaScript et SQL/DuckDB), rendez-vous sur ce classeur Observable.
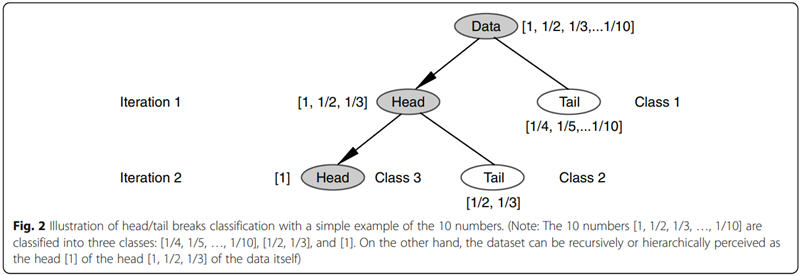
Considérons par exemple 10 nombres [1, 1/2, 1/3…1/10] (ou [1, 0.5, 0.333…0.1]) qui suivent cette règle de proposer plus de petites valeurs que de grandes.
La somme de cette série fait 2,93, la moyenne 0,293. 1, 1/2 et 1/3 lui sont supérieurs.
Si l’on divise la série en deux morceaux autour de la moyenne (« Head » au-dessus, « Tail » en dessous), on obtient donc l’itération 1 de cette figure :
L’algorithme Head/tail itère jusqu’à ce que cette division par la moyenne s’arrête, par exemple parce que le dernier « head » n’a plus qu’un élément ; ou que le dernier « head » a un effectif supérieur à son « tail », signe que la division n’est plus pertinente.
Head/tail fournit une alternative à la méthode de discrétisation de Jenks, bien plus rapide à calculer et, pour son concepteur, mieux apte à rendre compte d’une hiérarchie, d’une structure fractale, caractéristique fréquemment rencontrée dans la nature et le « vivant ».
Pour rappel, la méthode de Jenks – dite aussi des « seuils naturels » – conduit à délimiter x groupes les plus homogènes possibles, et en même temps les plus distincts les uns des autres. x est un paramètre fourni à l’algorithme de Jenks. Cet algorithme est de complexité O(n2), c’est-à-dire que son coût est proportionnel au carré de l’effectif de la distribution à classifier ; il devient difficile à calculer en JavaScript quand n dépasse 10 000 observations.
À l’inverse, la méthode Head/tail est de complexité O(n), et s’exécute en moins d’une seconde avec plusieurs millions d’observations. De plus, elle détermine – intelligemment – son propre nombre de classes, indicateur de la profondeur de la hiérarchie détectée (nombre que l’on peut toutefois réduire en ne retenant que les x premiers seuils).
Pour aller plus loin
- Page Wikipedia avec une liste d’implémentations dans divers langages (R, Python…)
- Jiang, B. (2013). « Head/tail breaks: A new classification scheme for data with a heavy-tailed distribution », The Professional Geographer, 65 (3), 482 – 494.
- Jiang, B. (2019). « A recursive definition of goodness of space for bridging the concepts of space and place for sustainability ». Sustainability, 11(15), 4091.
- Jiang, B. (2013) Geospatial Analysis Requires a Different Way of Thinking: The Problem of Spatial Heterogeneity
- Denise Pumain, Hierarchy in Natural and Social Sciences, Springer, 2006
- Thomas Ansart, Atelier de cartographie de Sciences-Po. Head/Tail breaks
- Éric Mauvière, classeur Observable Head/tail breaks
- L’outil Magrit et la librairie JS statsbreaks supportent Head/Tail
- Jean de La Fontaine, La tête et la queue du Serpent
Hyper intéressant, merci Éric.
Merci beaucoup, Claire !
Petite correction : la somme de cette série fait 2,93, la moyenne 0,293. 1, 1/2 et 1/3 lui sont *supérieurs*.
Merci pour votre relecture attentive, c’est corrigé !
Merci beaucoup, voilà de quoi laisser Jenks plus souvent au chaud cet hiver !